Register Login
Python Photoshop SAP Java PHP Android C++ Hadoop Oracle Interview Questions Articles Other

Binary Search in JavaScript

Updated Jan 16, 2023

Multiple algorithms and data structures that exist in programming can help programmers make the searching technique more efficient and easy. The method of searching using programming codes is one of the most typically performed operations in the field of Computer Science.

This article will show users the widely used technique of binary search in JavaScript.

What is Binary Search?

The binary search is an algorithm that splits the array approximately in half every time it checks or goes through the array element and checks whether the element exists in the JS array. When users search for a random element in the JS array, it undergoes this divide-and-conquer algorithm. The algorithm will divide the array into simple parts and execute the search algorithm.

There are certain criteria that programmers can follow to understand better how the search algorithm works. These are the steps that define the algorithm:

  • First, users find the central item of the given array.
  • Then, they need to compare the central item of that array with the element they are looking for, known as the key.
  • While searching the JS array, if the item is present in the left half of the JS array, users have to search in the left half.
  • Users search in the right half of the array if the key exceeds the central element.
  • But if the key is equal to the central element, it will return the index of that element of the JS array.
  • Users can continue with the first and the second steps until they get the single element.
  • If they do not find the key element, they can return -1.

Example of the searching algorithm:

Let us consider an array "arr" and insert some elements within it:

arr: 2 5 7 10 13 15 20 25 30

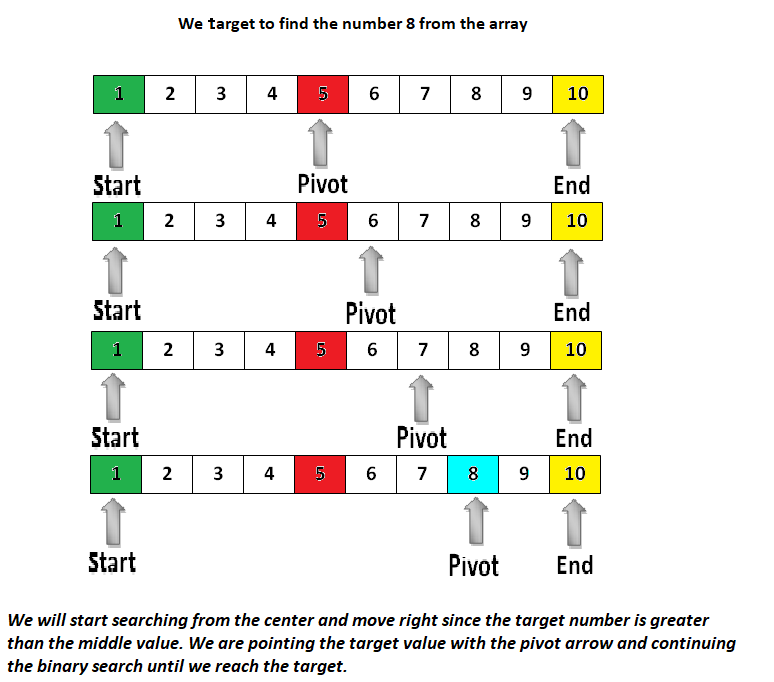
We consider that a user needs to search for the number 15 from the list of elements. First, we will encounter the middle element of the array.

Here, the central array element is 13. At the first search, if the key matches, we will return 1. If the key is larger than the number (yes, 15 is larger than 13), we will continue searching to the right half of the array.

Similarly to the first split, programmers can keep splitting the array until they search and get the element or finalize the array by ending up with one element as the key.

Code Snippet of the Binary search in JavaScript: 

<html>
<head>
<title>Binary Search in JavaScript</title>
</head>

<body>
<script>
let func = function (array, c, a, b) {
	// This is the Base Condition
	if (a > b) return false;
	// Here, we are finding the middle element
	let middle=Math.floor((a + b)/2);
	// Here, we are comparing the middle element with given key c
	if (array[middle]===c) return true;
	// If, during the search, the middle element is greater than c,
	// it will search in the left half of the array
	if(array[middle] > c)
		return func(array, c, a, middle-1);
	else
		// If the element in the middle is smaller than c,
		// search in the right half of middle
		return func(array, c, middle+1, b);
}
	
let array = [2, 5, 8, 9, 11, 15];
let c = 5;

document.write("Find key: " + c + " in array: " + array);
if (func(array, c, 0, array.length-1)){
	document.write("<br>Find the key!");
}else{
	document.write("<br>Cannot find the key!");
}

c = 6;
document.write("<hr>Find key: " + c + " in array: " + array);
if (func(array, c, 0, array.length-1)){
	document.write("<br>Find the key!");
}else{
	document.write("<br>Cannot find the key!");
}
</script>
</body>
</html>

Output:

Run Code Snippet

Explanation:

Here, we are using the Math.floor() function of JavaScript that compares the middle value with the key of the JS array. Then we called the func function that prints "Found the key!" when the key is present in the array and prints "Cannot find the key!" when the key is not present.

The efficiency of Binary Search:

In the binary search, the time complexity is O(log2n), where n denotes the number of items in the array. This technique will be better than the Linear Search, having a time complexity of O(n).

The Binary Search is an in-place algorithm like numerous other algorithms for searching. It suggests that the algorithm operates directly on the original array without generating its copies. But the users should note that the Binary search works only on sorted arrays.

Conclusion:

Here the article concludes that binary search is simple, reflexive, and efficient in logical search and easy implementation makes it a prevalent algorithm to explain the divide-and-conquer approach.

Recommended Posts:
×