Introduction to what Searching is & why we need searching:
Finding an object in a collection of different or same types of objects is known as a search. It involves the comparison between the given object and all other objects. If a match is found then we are done with the searching and there onward no need to compare.
There are many scenarios in software development where some data has to be located in a large collection of data. Some good examples of searching are file system search on desktop, web search engines etc. Here, we need a fast method to efficiently search for an object in a collection of millions of different data objects.
What is Binary Search
Binary search is an algorithm that is used to efficiently search an element in a sorted array of elements. It is based on dived and conquer algorithm. In this method at every step, search space is reduced by a factor of two. There is no need for any search operation to be performed in half of the array after every iteration of the search operation.
There are two methods to implement a binary search algorithm as
- Iterative Binary search
- Recursive Binary Search
Binary Search Template:
This is an example of the syntactic structure of how binary pseudo code looks like:
def BinarySearch(array)->int:
def condition(value)->bool:
pass
left,right=min(SearchSpace),max(SearchSpace)
while left<right:
mid=left+(right-left)//2
if condition(mid):
right=mid
else:
left=mid+1
return left
Complexity:
The time complexity of Binary search is.
- Best case complexity:O(1)
- Average case complexity:O(log n)
- Worst-case complexity:O(log n)
Space Complexity of Binary search is O(1).
Proof:
The recursive function is T(n)=T(n/2)+1
Put n=n/2 T(n/2)=T(n/4)+1+1
Putting the value of the T(n/2) above T(n)=T(n/4)+1+1 . . . . T(n/2^k)+1+1+1.....+1
=T(2^k/2^k)+1+1....+1 up to k
=T(1)+k
As we have taken 2^k=n K=log n
So, Time complexity is O(log n)
Explanation:
In best case element can be found in the middle of the list with a best-case complexity of O(1). In the worst case, there is a total log(n) comparison with the time complexity of log(n). On average there is log(n) time complexity.
Advantages of Binary search
Some of the advantages of Binary search are as:
- Time complexity is better than linear search.
- Efficient in case of the large collection of data.
Disadvantages of Binary search:
Some of the disadvantages of Binary search are as:
- The list must be sorted in the increase or decrease order.
- The complexity of the program increases in the case of data structures where no random access to the elements is possible such as linked list, stack etc.
- The implementation of Binary search is more difficult than linear search. More lines of code are needed to implement binary search.
Algorithm and Stepwise representation of Binary Search:
Binary Search is based on the divide and conquers concept. On the list, set two points to the first and last element of the list as 0 and the size of the list. Recursive calculate the middle pointer and check if the element is present in the middle. If the element is present then the binary search is over.
If the element is not matched then set the left and right points as per logic where can the element can lay between left to middle space and middle to right half-space.
There are the steps in case of elements of the list are sorted in increasing order.
- While the left point is small then the right point repeats the following steps.
- Find the middle point between the left and right points.
- Check if the element matches the element at the middle pointer. If matches then return the index of the middle point.
- Else Check if the element at the middle point is small than the element to be matched. If the element is smaller set the last pointer to middle pointer -1.
- Else set the first pointer to middle pointer +1
In case of the element are sorted in decreasing order the last two conditions have to be modified as per the logic of the Binary search algorithm.
How it is Different from linear search:
A linear search is a brute-force approach to search. It tries to match every element of the list. If it is lucky then it may find it in its first search but in some cases, it has to travel the whole list if the element is present at the end.
Binary search is a smart way of searching where we divide the search space in every iteration. So, in the worst case, there is only a log(n) comparison.
| Linear search | Binary Search |
|---|---|
| Compare with each element of the list. | Compare with only the log(n) element of the list. |
| The list not needed to be sorted. | To apply Binary search list must be sorted. |
| Apply all types of data structures with the same complexity. | High complexity in case of data structures where random excess of the element is not possible. |
| Based on an iterative approach. | Based on dived and conquer algorithm. |
| Used in case of the small data set. | Use in case of a large database. |
Program for Binary search (normal/iterative program):
Binary search can be implemented iteratively with the help of a while loop. Apply the condition left < right in the while loop. Inside the while loop calculates the mid-value and checks if the element is present in mid or not. After that set left and right as per logic.\
Syntax:
mid=(low+high)/2
if(x==arr[mid])
return mid
elseif(x>arr[mid])
low=mid+1
else
high=mid-1
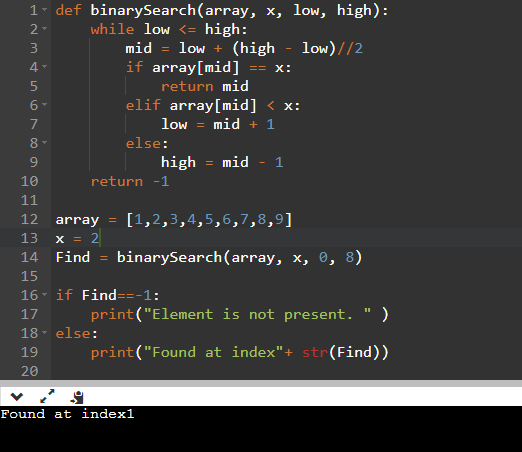
Program:
defbinarySearch(array,x,low,high):
whilelow<=high:
mid=low+(high-low)//2
ifarray[mid]==x:
returnmid
elifarray[mid]<x:
low=mid+1
else:
high=mid-1
return-1
array=[1,2,3,4,5,6,7,8,9]
x=2
Find=binarySearch(array,x,0,8)
ifFind==-1:
print("Elementisnotpresent.")
else:
print("Foundatindex"+str(Find))
Explanation:
Here, First, define a function binarySearch that implements the Binary search algorithm. This function tack three variables array, x the element which has to be searched low pointer and high pointer. Inside the function apply the Binary search iterative logic.
After then declare a variable array and x with value 2. Call the function binarySearch and store the value returned by it in the find variable. At last, check if the element is found or not.
Recursive program for Binary Search:
Binary Search can also implement recursively. By setting the base condition as left>right return-1. In recursive function Find the middle value and check if the element match or not. Else recursive try to call for half search space for the match.
Syntax:
binarySearch(arr, x, low, high)
if low > high
return False
else
mid = (low + high) / 2
if x == arr[mid]
return mid
else if x > arr[mid]
return binarySearch(arr, x, mid + 1, high)
else
return binarySearch(arr, x, low, mid - 1)
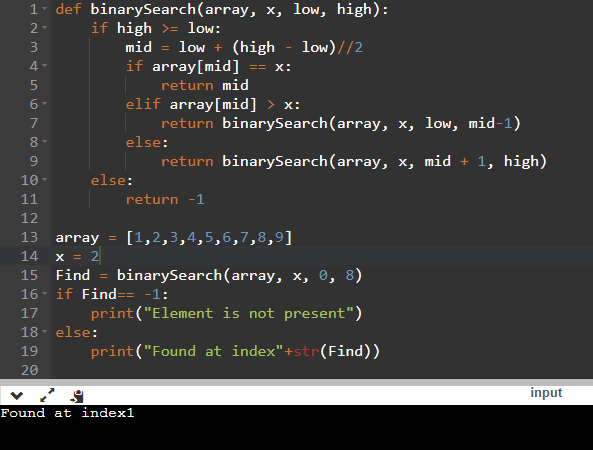
Program:
def binarySearch(array, x, low, high):
if high >= low:
mid = low + (high - low)//2
if array[mid] == x:
return mid
elif array[mid] > x:
return binarySearch(array, x, low, mid-1)
else:
return binarySearch(array, x, mid + 1, high)
else:
return -1
array = [1,2,3,4,5,6,7,8,9]
x = 2
Find = binarySearch(array, x, 0, 8)
if Find== -1:
print("Element is not present")
else:
print("Found at index"+str(Find))
Explanation:
Here, First, define a function binarySearch that implements the Binary search algorithm. This function tack three variables array, x the element which has to be searched, low pointer and high pointer. Inside the function apply the Binary search Recursive logic.
After then declare a variable array and x with value 2. Call the function binarySearch and store the value returned by it in the find variable. Last, check if the element is found or not.
Conclusion:
We hope this article has given you a crisp idea of what is searching and why we need to search, what is Binary Search, the complexity in binary search, its advantages & disadvantages, the algorithm and steps to perform binary search (how it works), how it is different from linear search, and recursive program for Binary Search. Binary Search gets implemented only if the values are sorted.
Otherwise sorting it separately using any sorting technique might increase the complexity of the entire program, making the program inefficient. But in case of sorted array values, this is the most efficient searching technique you can use.