Do you know that Dijkstra's algorithm helps in navigating the efficient route and effective suggestions in booking flights? It turns out that you already have implemented Dijkstra's algorithm in your daily life. This article will guide you through a complete walkthrough of Dijkstra's algorithm and how to easily implement it in Python.
What is Dijkstra's algorithm?
Dijkstra's algorithm is a graph-simplification algorithm that helps in finding the shortest paths between the starting node and the ending node in a graph. In the year 1956, a Dutch programmer Edsger W.
Dijkstra came up with a question. He wanted to calculate the shortest path to travel from Rotterdam to Groningen. He did not seek the help of the map to measure the distances of the roads. Rather he took a computer scientist’s approach. He started determining a graph with vertices and edges such as traveling from city A to city B (where A and B are two vertices).
That allowed Mr. Dijkstra to explore the more universal problem of graph search. That brings in the concept of finding the shortest path using Dijkstra’s algorithm.
In computer science, there are a lot of problems that this algorithm solves. Many apps like Zomato, Uber, Flight navigators, Google Map, etc., solve their most efficient path algorithm program by finding the shortest path between two points through Dijkstra's algorithm. This popular search algorithm is a part of data structure and uses theoretical calculations using a graph. Another popular use of Dijkstra's algorithm is in routing protocols used in routers.
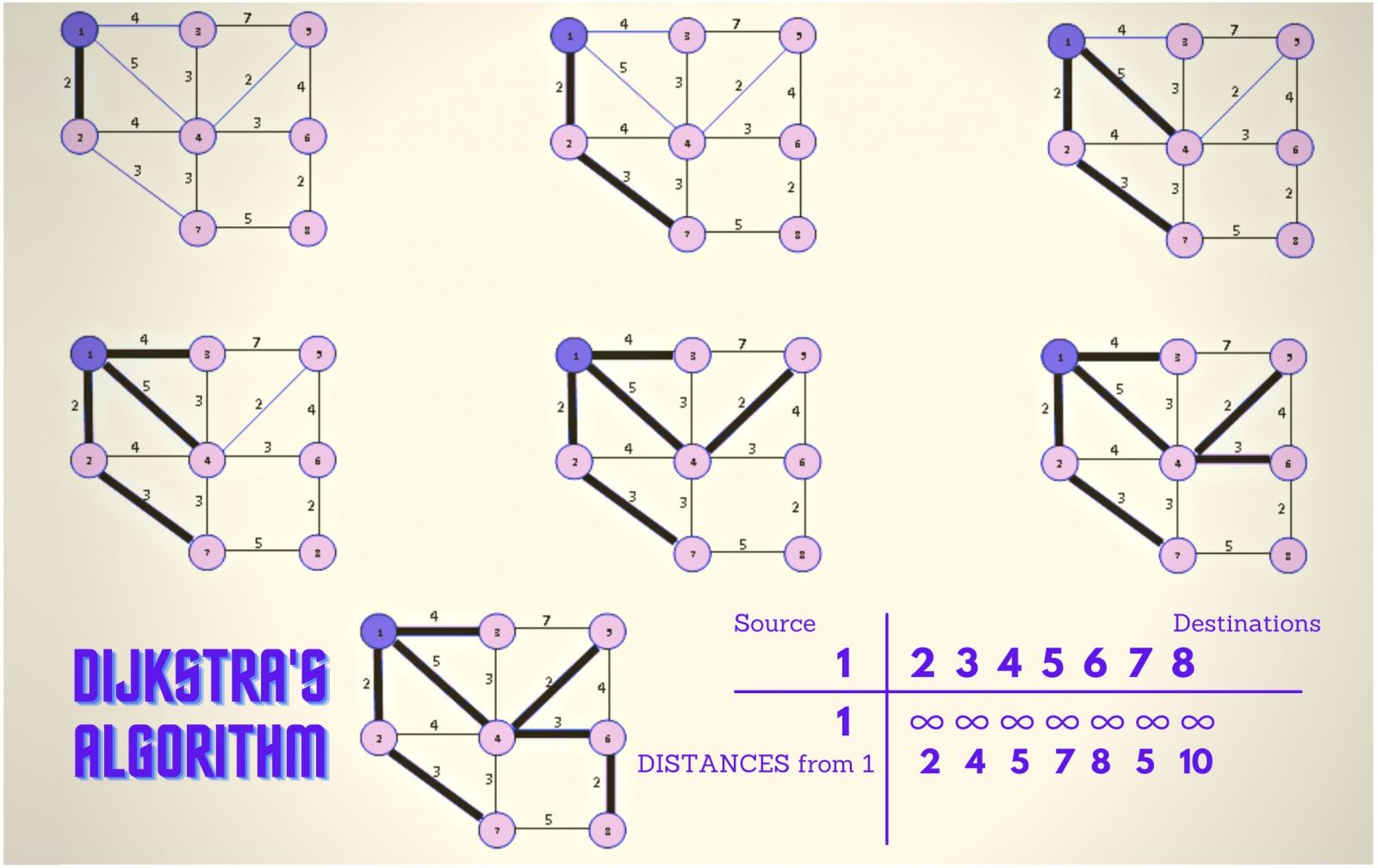
How Dijkstra’s Algorithm works?
The steps are:
- First initialize the starting point (vertex) for the path to traverse.
- Then we have to set all the weights for each edge of the graph.
- Next, from the starting graph, we will check all the nearest vertices that are directly connected from the source graph.
- We will then set the calculate their edges and set the weights for each of these nearby vertices.
- From these nearby vertices, we will then check other vertices that will have the least weight or we can say the shortest path.
- We add the values of those edges and prepare the summation for each of them to calculate the shortest path from the source to all other vertices as shown in the figure above.
- From the source vertex, we will have to ultimately find the shortest possible path to all other vertices (where each of them are destinations vertices).
Program:
import sys
class OperatingGrap():
def __init__(self, vert):
self.V = vert
self.graph = [[0 for column in range(vert)]
for row in range(vert)]
def printVal(self, distn):
print(" Measuring the Distance of the Vertex from Source ")
for n in range(self.V):
print(n, "t", distn[n])
def minDistance(self, distn, sptSet):
min = sys.maxsize
for v in range(self.V):
if distn[v] < min and sptSet[v] == False:
min = distn[v]
min_index = v
return min_index
def dijkstraAlgo(self, src):
distn = [sys.maxsize] * self.V
distn[src] = 0
sptSet = [False] * self.V
for cout in range(self.V):
u = self.minDistance(distn, sptSet)
sptSet[u] = True
for v in range(self.V):
if self.graph[u][v] > 0 and sptSet[v] == False and distn[v] > distn[u] + self.graph[u][v]:
distn[v] = distn[u] + self.graph[u][v]
self.printVal(distn)
go = OperatingGrap(9)
go.graph = [[0, 4, 0, 0, 3, 0, 0, 8, 0],
[4, 0, 8, 0, 0, 0, 0, 11, 0],
[0, 8, 0, 7, 0, 4, 0, 0, 2],
[0, 0, 7, 0, 9, 12, 0, 0, 0],
[0, 0, 0, 9, 0, 10, 0, 0, 0],
[0, 0, 4, 12, 11, 0, 3, 0, 0],
[0, 0, 0, 0, 0, 2, 0, 1, 8],
[8, 10, 0, 0, 0, 0, 1, 0, 6],
[0, 0, 1, 0, 0, 0, 5, 10, 0]
]
go.dijkstraAlgo(0)
Output:

Explanation:
First we will import the sys module. Then we will create a class with the name OperatingGrap. Next, we define the __init__ and prepare the vertex and the graph and set the graph from 0 till the column in range of ‘vert’. Then we use the for loop to to bring all the vertex in the row one by one.
We then create another user-defined function printVal() that accepts the distance of the vertex from the source as parameter. Then we use the for loop to display all the vertex distance one by one using the print() function.
Next, we create another user-defined function minDistance() and pass the minimum distance value along with the set of vertices not yet included in shortest path tree (sptSet). Then we have to initialize the minimum distance for next node using the sys.maxsize. The next for loop will search for the nearest vertex in the shortest path tree and will assign it (the variable v) to the min_index variable. The user-defined function finally returns the min_index’s value.
Then we have a user-defined function that implements Dijkstra's single source shortest path algorithm for a graph represented using adjacency matrix representation. It picks the minimum distance vertex from the set of vertices that are not yet processed. The for loop within the function is picking the minimum distance vertex and checking if it is the shortest route from the given starting vertex or not.
The statement distn[v] = distn[u] + self.graph[u][v] is increasing the distance count (by adding with the previous distance) if the value of distn[v] is greater than distn[u] + self.graph[u][v]. In other words, we can say that the code updates the dist value of the adjacent vertices of the picked vertex only if the current distance is greater than new distance plus the vertex isn’t in the shortest path tree.
Outside the function, we create the object go and make a graph of size 9x9 by creating a list within another list. Then, through the go object of the class, we will call the dijkstraAlgo() and pass the argument (vertex) that we want to be the initial/source vertex.
Conclusion:
The graph is a very well-used data structure that helps in visualizing and solving a lot of data structure and algorithmic problems in mathematics and computer science.
Dijkstra's algorithm finds the shortest path from one vertex to the rest and is popularly used in various modern apps and web applications. Implementing it in Python is another significant utility that helps many Python developers leverage its use in other larger Python-driven applications.