Sorting is an essential part of many applications that allows us to sort our data in ascending or descending order. QuickSort is one of the sorting algorithms that use a Divide and Conquer principle.
This article will guide you with the step by step process in the QuickSort algorithm and will help you:
- Understand QuickSort algorithm
- QuickSort implementation in Python
- Applications of QuickSort
- Time and Space complexity in QuickSort algorithm
Understanding QuickSort algorithm:
The QuickSort algorithm follows the Divide and Conquer principle, where an array is divided into sub-arrays by selecting a pivot element from the array. The array is divided after the pivot element is placed in the array in such a position that the elements less than the pivot element are placed at the left and elements greater than the pivot element are placed at the right.
The left and right part of the array is also divided using the same technique and is continued until each sub-array contains only one element. This also indicates that the array is sorted.
QuickSort algorithm steps:
1. Consider an array, arr = [10, 80, 30, 90, 40, 50, 70], a variable pivot, i and j with the following values:
pivot = 70 (any one element from the array can be considered as pivot element) i = -1
j = 0
2. The pivot element is compared with each element in the array starting from the element at 0th index.
3. On iteration, if the element is less than or equal to the pivot element then the value of i is incremented and elements present at position i and the element present at position jare swapped, else, if the element is greater than the pivot element, then iterate to the next element.
4. Iteration1:
Initial values: i = -1 and j = 0
Since, arr[j] < pivot so, i increments to become 0 and arr[i] and arr[j] are swapped Final values: i = 0 and j = 0
Result: [10, 80, 30, 90, 40, 50, 70]
5. Iteration2:
Initial values: i = 0 and j = 1
Since, arr[j] > pivot so just iterate to the next element Final values: i = 0 and j = 1
Result: [10, 80, 30, 90, 40, 50, 70]
6. Iteration3:
Initial values: i = 0 and j = 2
Since, arr[j] < pivot so, i increments to become 1 and arr[i] and arr[j] are swapped Final values: i = 1 and j = 2
Result: [10, 30, 80, 90, 40, 50, 70]
7. Iteration4:
Initial values: i = 1 and j = 3
Since, arr[j] > pivot so just pass to the next element Final values: i = 1 and j = 3
Result: [10, 30, 80, 90, 40, 50, 70]
8. Iteration5:
Initial values: i = 1 and j = 4
Since, arr[j] < pivot so, i increments to become 2 and arr[i] and arr[j] are swapped Final values: i = 2 and j = 4
Result: [10, 30, 40, 90, 80, 50, 70]
9. Iteration6:
Initial values: i = 2 and j = 5
Since, arr[j] < pivot so, i increments to become 3 and arr[i] and arr[j] are swapped Final values: i= 3 and j = 5
Result: [10, 30, 40, 50, 80, 90, 70]
10. Iteration7:
Initial values: i = 3 and j = 6
Since, arr[j] = pivot so, i increments to become 4 and arr[i] and arr[j] are swapped Final values: i = 4 and j = 6
Result: [10, 30, 40, 50, 70, 90, 80]
With this, we have the pivot element, 70 at the sorted position, that is, all the elements placed at the left of the pivot element are lesser than pivot element and all elements at the right of the pivot element are larger than the pivot element.
Now, applying the same process to the left and right arrays of the pivot element we get the sorted array.
Final result: [10, 30, 40, 50, 70, 80, 90]
QuickSort implementation in Python
def partition(array, min, max):
pivot = array[max]
i = min - 1
for j in range(min, max):
if array[j] <= pivot:
i = i + 1
(array[i], array[j]) = (array[j], array[i])
(array[i + 1], array[max]) = (array[max], array[i + 1])
# return the position from where the partition is done
return i + 1
def quickSort(array, min, max):
if min < max:
sub_array = partition(array, min, max)
quickSort(array, min, sub_array - 1)
quickSort(array, sub_array + 1, max)
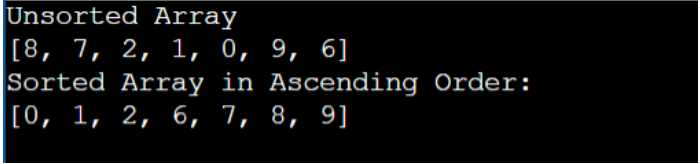
array = [8, 7, 2, 1, 0, 9, 6]
print("Unsorted Array")
print(array)
size = len(array)
quickSort(array, 0, size - 1)
print(' Sorted Array in Ascending Order: ')
print(array)
Output:
Explanation:
First we create a user-defined function to find the partition position and pass three parameters within it. Then we consider last element as the pivot element and place it in the pivot variable. Next, we use a pointer ‘i’ to check the greater element. Then we have used a for loop to traverse the array and compare each element with pivot element.
Then we perform a condition check if the element is smaller than pivot element then swap it with greater element pointed by i. Then we perform the swapping of element from I to j using this (array[i], array[j]) = (array[j], array[i]) statement. Next we can swap the pivot element with the greater element specified by I and return the position from where the partition is done.
Next we create another user-defined function to perform quicksort(). Inside the function, we define the statements for finding the pivot element such that element smaller than pivot are on the left and element greater than pivot are on the right. Then we perform the recursive call on the left of pivot
quickSort(array, min, sub_array - 1)
and same for the right one as well.
Finally, we take a list in the array variable and print the unsorted list first and then use QuickSort(), passing the list as parameter to perform the sorting.
Applications of QuickSort:
- Used for sorting data like
-
- sorting files by their name, date, price,
- Sorting students data by their roll no,
- Sorting account profile by id, and so on
-
- Used for quick information searching as QuickSort algorithm is the fastest algorithm
Time and Space complexity in QuickSort algorithm
- Time complexities:
-
- O(n2): This occurs when the pivot element selected is the shortest or the largest
- O(n*log n): This occurs when the pivot element is the middle element.
-
- Space complexity: O(log n)